Direct Uncertainty Prediction for Medical Second Opinions

The Challenge of Doctor Disagreements

In many different domains, it is common for human experts to disagree with each other significantly. One such domain is medicine, where two doctors looking at the same patient data may come to very different conclusions about the diagnosis and potential next steps.

A wealth of clinical research has shown that this problem is prevalant across many different medical specialties, from breast cancer diagnosis via biopsy (25% disagreement) to identifying tuberculosis, where radiologists disagree with other colleagues 25% of the time and themselves 20% of the time, to ophthalmology cases when determining Diabetic Retinopathy.

Machine Learning for Medical Second Opinions

A natural question when seeing these statistics is whether these disagreements arise solely as a result of random errors. This isn’t quite the case. Below, we show individual doctor diagnoses for two different patients from our data. For patient 2, all the doctors agree on the diagnosis, while for patient 1, there is significant variation on what the diagnosis should be. (Interestingly, when a careful consensus scoring was conducted, both patients ended up with the same diagnosis.)

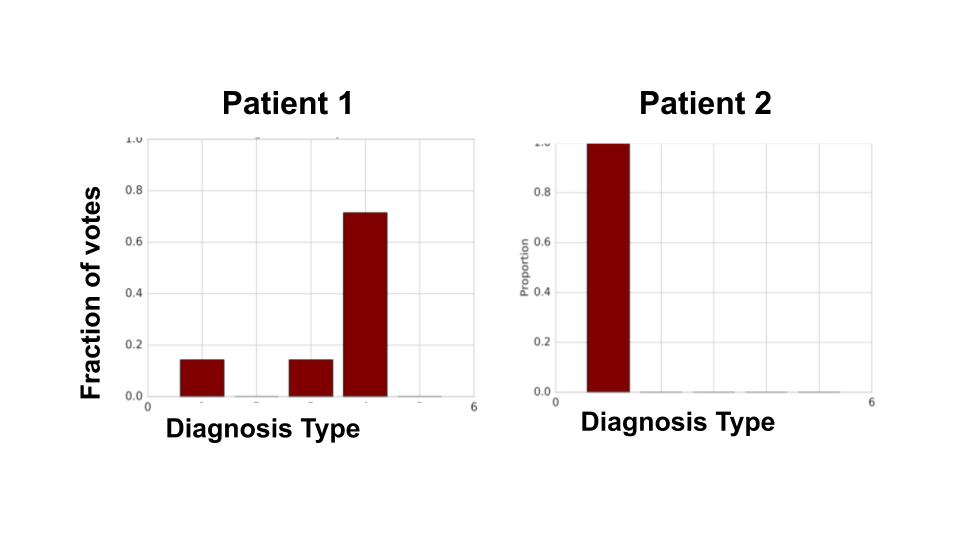
This suggests there are features in the patient data that highly influence doctor disagreement. If such predictive features exist, we can try to use machine learning to identify the cases that might cause large disagreements. Such cases could be flagged for a medical second opinion.

Direct Uncertainty Prediction (DUP) and Uncertainty Via Classification (UVC)

Machine learning and particularly deep learning often use a model (a neural network) that acts as a classifier, used to categorize inputs into different classes, or in the case of medical applications, diagnose the severity or type of disease.

Concretely, given an input \(x\), the classifer outputs a distribution \((\hat{p}_1,...\hat{p}_n)\) over the n possible classes. For inputs \(x\) where we have multiple (noisy) labels (e.g. multiple individual doctor diagnoses), the target output is the empirical distribution of those labels, \((p_1,...,p_n)\).

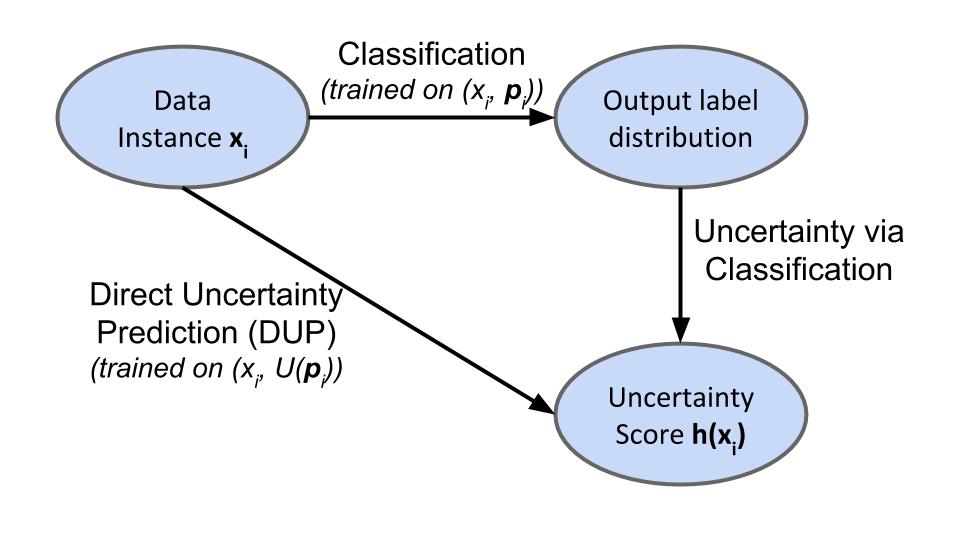
A first method of identifying whether the example \(x\) might give rise to uncertainty is to compute a measure of spread, \(U(\cdot)\) over the predicted distribution \((\hat{p}_1,...\hat{p}_n)\). We call this Uncertainty via Classification (UVC).

For example we could compute the variance of the distribution \(U_{var}((p_1,...,p_n))\), or its entropy, \(U_{ent}((p_1,...,p_n))\), or the chance of disagreement, \(U_{disagree}((p_1,...,p_n)) = 1 - \sum p_i^2\).

Alternatively, if we have a target measure of spread \(U(\cdot)\), in mind, we can also train a new model directly on the scalar uncertainty score \(U((p_1,...,p_n))\). We refer to this scheme as Direct Uncertainty Prediction (DUP). Below is a schematic of both methods:

Understanding the Unbiasedness of DUP with a Mixture of Gaussians Example

In many settings, the machine learning model sees only a subset of the full input that the human expert uses to make their decision. For example, a doctor may see an image as well as patient’s full medical history, while the model only sees the image.

In such a setting, where there are latent features, performing DUP gives an unbiased estimate of the uncertainty score, while UVC has a bias term, overestimating the inherent uncertainty. The full statement of the theorem and proof can be found in the paper. Below, we’ll work through some of the intuition with a very simple example using a mixture of two Gaussians.

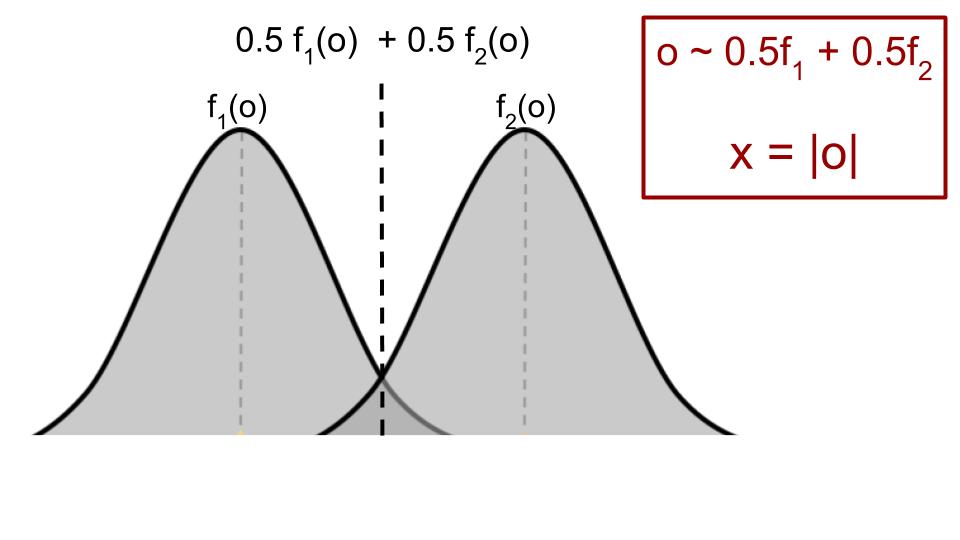
Suppose the full input \(o\) that is only seen by the human expert is drawn from a mixture of two 1d Gaussians, with means \(\pm1\), variance \(1\) and mixture probability \(0.5\). The model only sees \(x=|o|\), the absolute value of \(o\).

Given \(o\), the true distribution \((p_1, p_2)\) over the two labels is given by

and the true uncertainty score over labels is \(U((p_1, p_2))\). For concreteness, let \(U = U_{disagree}\), and so the inherent uncertainty for \(o\) is \(1 - p_1^2 - p_2^2\).

If we only see \(x = \lvert o \rvert\), then with \(0.5\) probability, the label distribution is \((p_1, p_2)\) (when \(x = o\)) and with \(0.5\) probability \((p_2, p_1)\) (when \(x = -o\)).

We’d like to predict \(U_{disagree}\) given \(x\). What do DUP and UVC do in this setting?

DUP directly predicts the target uncertainty. But this is either \(1 - p_1^2 - p_2^2\) (with \(0.5\) probability when \(x = o\)), or \(1 - p_2^2 - p_1^2\) (the same value) when \(x = -o\). In particular, due to symmetry, the sign of \(o\) doesn’t matter for the uncertainty score and so DUP gives a perfect prediction.

What about UVC? The sign of \(o\) does matter (critically) for the full label distribution, which is either \((p_1, p_2)\) (when \(x = o\)) or \((p_2, p_1)\) (when \(x = -o\)). So UVC predicts the label distribution as \(0.5(p_1, p_2) + 0.5(p_2, p_1) = (0.5, 0.5)\) and uses this to give a trivial, constant prediction of \(0.5\) as the uncertainty score.

In the paper, we prove a general theorem that in the presence of hidden information, DUP will outperform UVC.

Synthetic Example with Image Blurring on SVHN and CIFAR-10

We study another synthetic example by blurring images of SVHN and CIFAR-10 to different degrees and drawing multiple labels for each image from a correspondingly noisy distribution. For instance, if the image is clean (not blurred at all), then the label distribution has all of its mass on the true label. Whereas if the image is severely blurred, significant mass is put on incorrect labels.

We use these labels to compute a target uncertainty score, using this and the empirical label distribution to train DUP and UVC models respectively. Again, we find that DUP outperforms UVC in predicting uncertainty scores. Interestingly, we see some evidence that DUP and UVC models are also paying attention to different features of the image.

Evaluation on a Large Scale Medical Imaging Task

Our main evaluation is on a large scale medical imaging task on diagnosing Diabetic Retinopathy (DR), from fundus photographs, large images of the back of the eye. DR is a disease caused by high levels of blood sugar damaging the back of the eye. Despite being treatable if caught early enough, it remains a leading cause of blindness.

DR is typically graded on a five class scale, from grade 1 (no DR) to grade 5 (proliferative DR). An important clinical threshold is at grade 3, with grades 3 and above corresponding to referable DR, requiring immediate specialist attention.

We train both DUP and UVC models on this dataset, where again all the DUP models outperform the UVC models on both the holdout set, as well as a special, adjudicated dataset which contains gold-standard consensus labels. On this second dataset, we evaluate our models with multiple metrics (agreement on referable grades, majority agreement with consensus, median agreement with consensus) and also perform a ranking study, finding that DUP consistently beats UVC.

Summary and Future Directions

Predicting human expert disagreement is a fundamental problem in many domains, and especially so in medicine, where a useful second opinion might significantly improve patient outcomes. In our work, we show that machine learning models can successfully predict human disagreements directly from the data, with Direct Uncertainty Prediction (DUP) providing a provably unbiased uncertainty score. We validate this method on both synthetic examples of Gaussian mixtures and image blurring of standard benchmarks, as well as a large scale medical imaging application in ophthalmology.

Full details and additional results are in our paper, Direct Uncertainty Prediction for Medical Second Opinions! We’re continuing with work exploring the implications for combining human and algorithmic expertise.

Acknowledgements: Thanks to Jon Kleinberg, Ziad Obermeyer and Sendhil Mullainathan for their feedback on this post.